# 学习历史
我大学并没有专门学过数据结构和算法的课,工作前几年碰到数据结构和算法相关的内容就有点发怵。也专门买过类似的数据结构和算法的书来看,但是总是感觉学的一般。
后来极客时间出了一个「数据结构和算法之美」的课程之后,系统看了一下,发现原来数据结构的学习并不是毫无章法的学习,而是有迹可循的。
不同的数据结构有不同的使用场景,了解一个数据结构的设计最重要的是搞清楚这个数据结构要解决的问题, 这样就能把握住这个数据结构的核心设计原则。至于对这个数据结构如何操作,那是第二步要学习的内容。
我之前学习数据结构的一个误区就是舍本逐末,只关注对数据结构的操作,并没有去关注数据结构到底要解决什么问题。
对数据结构的操作无非也就是增删改查,而数据结构的不断进化也是围绕着提升这4个操作的执行效率的(这也是要搞清楚时间复杂度和空间复杂度这些基本概念的原因)。
# 梳理数据结构
简单聊一下我对一些常见的数据结构的理解
# 数组
数组是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
它的特点是
- 随机访问。根据下标随机访问的时间复杂度为 O(1)
- 通过遍历的方式进行查找,时间复杂度为 O(n)
- 插入删除比较低效,为了保证内存空间的连续,需要在增加和删除元素的同时,搬运其余部分元素。
# 链表
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。
在链表里除了存储要保存的元素,还要在节点上额外保存只向下一个节点的指针信息。
如果单纯看链表的特性,似乎并没有什么值得看的,所以对比数组看,链表相对于数组究竟优化了哪些点,解决了什么问题。
# 数组 VS 链表
相对于数组来说,链表最重要的改进是,提高了插入和删除元素的效率。同时链表有很多的变体,比如循环链表,双向链表等。但是链表也有一些操作的性能不如数组,比如随机访问。
依次列一下两个数据结构的对比。
- 相对于数组来说,链表的查询效率并没有提高太多,查找某个元素依然是需要遍历整个链表,O(n) 的时间复杂度。
- 链表的插入和删除给定指针元素(不需要遍历)的时间复杂度为 O(1) ,而数组执行同样操作的时间复杂度是 O(n)。
- 随机访问第 X 个元素,数组时间复杂度为 O(1),链表则为 O(n)
其实从链表这儿开始就开始接触更加复杂的数据结构了。
# 栈
栈是一种抽象的数据结构,它进行入栈(push)和出栈(pop)的运算。栈并没有暴露查找这些功能,大家一般也不会在栈上进行查找。
栈一般是通过数组和链表实现的,相对于数组来说栈暴露的接口少,程序员使用的时候不容易出现误操作。栈最为人所熟知的使用场景是,函数调用时使用的栈,注意这里只是概念很相似,内存中的堆栈和数据结构堆栈不是一个概念,可以说内存中的堆栈是真实存在的物理区,数据结构中的堆栈是抽象的数据存储结构。
关于使用函数调用栈来保持临时变量的讨论 我们不一定非要用栈来保存临时变量,只不过如果这个函数调用符合后进先出的特性,用栈这种数据结构来实现,是最顺理成章的选择。 从调用函数进入被调用函数,对于数据来说,变化的是什么呢?是作用域。所以根本上,只要能保证每进入一个新的函数,都是一个新的作用域就可以。而要实现这个,用栈就非常方便。在进入被调用函数的时候,分配一段栈空间给这个函数的变量,在函数结束的时候,将栈顶复位,正好回到调用函数的作用域内。
# 队列
队列是一种抽象的数据结构,和栈类似,它进行入队(enqueue)和出队(dequeue)的运算。
跟栈一样,队列可以用数组来实现,也可以用链表来实现。
# 散列表
散列表,又叫做字典、哈希(hash)表,用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。可以说,如果没有数组,就没有散列表。
相对于数组,散列表引入了key-value 的概念来提高数组的查询效率。当然从另外一个角度来说,数组的下标也可以作为 key 来使用。所以在散列表里除了存储要保存的元素,还要额外保存键信息。
散列函数的查找过程是,通过散列函数 hash(key) 来计算出数组的下标,最后利用数组随机访问的特性,通过下标直接访问元素。
# 散列冲突
这里需要关注散列冲突的问题,即两个不同的键值(key)通过散列函数计算后得到的散列值相同的问题。事实上并没有完美的无冲突的散列函数(我认为本质上是数据空间的问题)。
两个散列冲突的解决方法
开放寻址法。开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。具体方法有线性探测、二次探测(Quadratic probing)和双重散列(Double hashing)。这里有空继续补充。
链表法。官方这张图非常好,一图胜前言。通过散列函数计算出散列值,如果出现散列冲突就往数组对应的链表后面继续追加,查找的时候在散列值对应的槽位链表处进行遍历。链表里的节点信息应该是包含原始 key 值的,否则查找时候只给定key值是没办法定位对应元素的。
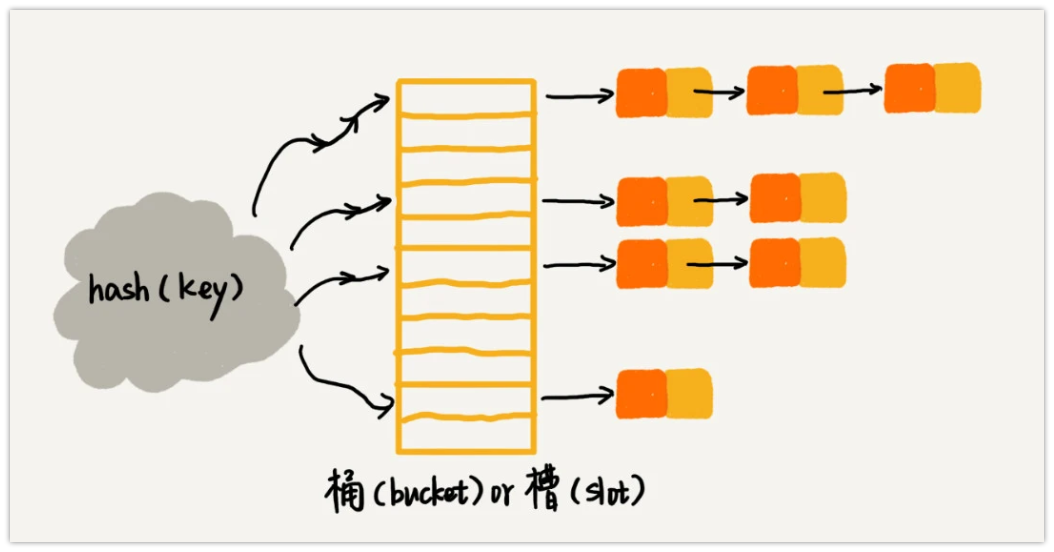
如果出现极端的散列冲突的情况,查找效率就会蜕变为遍历链表的时间复杂度 O(n),为了解决这个问题,这里的链表会更改为更「高级」的数据结构红黑树。
# 数组 VS 字典
相比于链表和数组,散列表能够大幅提升数据集合的增删改查速度。
# 二叉树
普通的二叉树似乎相对于散列表并没有什么太多的优势,但是有一些结构化的二叉树是很有用的,比如二叉查找树,平衡二叉查找树(红黑树)。
# 平衡二叉查找树 vs 散列表
- 需要按顺序输出数据集合的时候,散列表需要做额外的排序操作,二叉查找树只需要中序遍历。
- 散列表遇到散列冲突时,性能不稳定,但是平衡二叉查找树的时间复杂度稳定在 O(logn),能满足大量数据生产场景的使用
- 散列表为了避免散列冲突,如果装载因子太小(表中元素个数/散列表长度),会浪费一定的存储空间。而为了设置合理的散列函数,以及解决散列表扩容缩容、散列冲突的问题,会使散列表构造的复杂度比二叉查找树要高。
这两者的最终选择还是要看具体的使用场景。
# 最后
大概梳理了一遍日常常用的数据结构,一般常用的数据结构基本上就这些了。还有更复杂的数据结构,比如图,不过我对这个数据结构不熟悉,不献丑了。
正常来说能搞清楚上面这些数据结构已经够日常开发使用了,深入理解这些数据结构的不同的特点,在不同的场景去用他们解决相关问题,这是数据结构的意义。
关注我的微信公众号,我在上面会分享我的日常所思所想。
