# 题目描述
接雨水 https://leetcode.cn/problems/trapping-rain-water/description/ (opens new window) 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6
# 暴力求解法
暴力求解的思路就是找到柱子左右最高的柱子,左右两根柱子中相对较低的那个决定了当前这个柱子能接到的最大的水量。
所以解决思路就是在遍历元素的时候,再次从元素左右两侧开始遍历,拿到左右两侧的最大值,得到当前元素最大「接水量」后,然后不断求和就好了..
代码如下,时间复杂度为 O(n^2)
func trap1(_ height: [Int]) -> Int {
var res = 0
for (index, value) in height.enumerated() {
var left = index - 1
var maxLeftValue = 0
while left >= 0 {
let leftValue = height[left]
maxLeftValue = max(maxLeftValue, leftValue)
left = left - 1
}
var right = index + 1
var maxRightValue = 0
while right < height.count {
let rightValue = height[right]
maxRightValue = max(maxRightValue, rightValue)
right = right + 1
}
let minValue = min(maxLeftValue, maxRightValue)
res = res + max(minValue - value, 0)
}
return res
}
# 暴力解法优化
既然要拿到某个元素左右两侧的最大值,那有没有更快地方法。可以通过遍历两遍数组,拿到某个元素位置(包含当前元素)的左侧最大值数组和右侧最大值数组。
举个例子,在数组 [4,2,0,3,2,5] 中,位置 0 处的值是 4,遍历后得到元素左侧最大数组 [4,4,4,4,4,5],遍历后得到的右侧最大值数组 [5,5,5,5,5,5]。
当我们想要计算某个元素最大节水量的时候,就直接去取当前元素左侧下标对应的左侧最大数组中的值,就是左侧最大值;同理计算右侧最大值。
计算接水量的逻辑是一样的..
代码如下
func trap(_ height: [Int]) -> Int {
var maxLeftArr = [Int]()
var maxLeft = 0
for (index, value) in height.enumerated() {
maxLeft = max(maxLeft, value)
maxLeftArr.append(maxLeft)
}
var maxRightArr = [Int]()
var maxRight = 0
for (index, value) in height.reversed().enumerated() {
maxRight = max(maxRight, value)
maxRightArr.append(maxRight)
}
maxRightArr.reverse()
var res = 0
for (index,value) in height.enumerated() {
if index == 0 || index == height.count - 1 {
//
} else {
let left = maxLeftArr[index-1]
let right = maxRightArr[index+1]
let minValue = min(left, right)
res = res + max(minValue - value, 0)
}
}
return res
}
# 单调栈解法
看卡哥的文章感觉卡哥这里介绍的关于单调栈的计算规则不是很清楚,在单调栈的计算方式里,如图黄色区域指向部分,这里的接雨水量是通过两部分组成的,第一部分是 Part1,第二部分是 Part2,这两部分组合起来就是总的接雨水量。
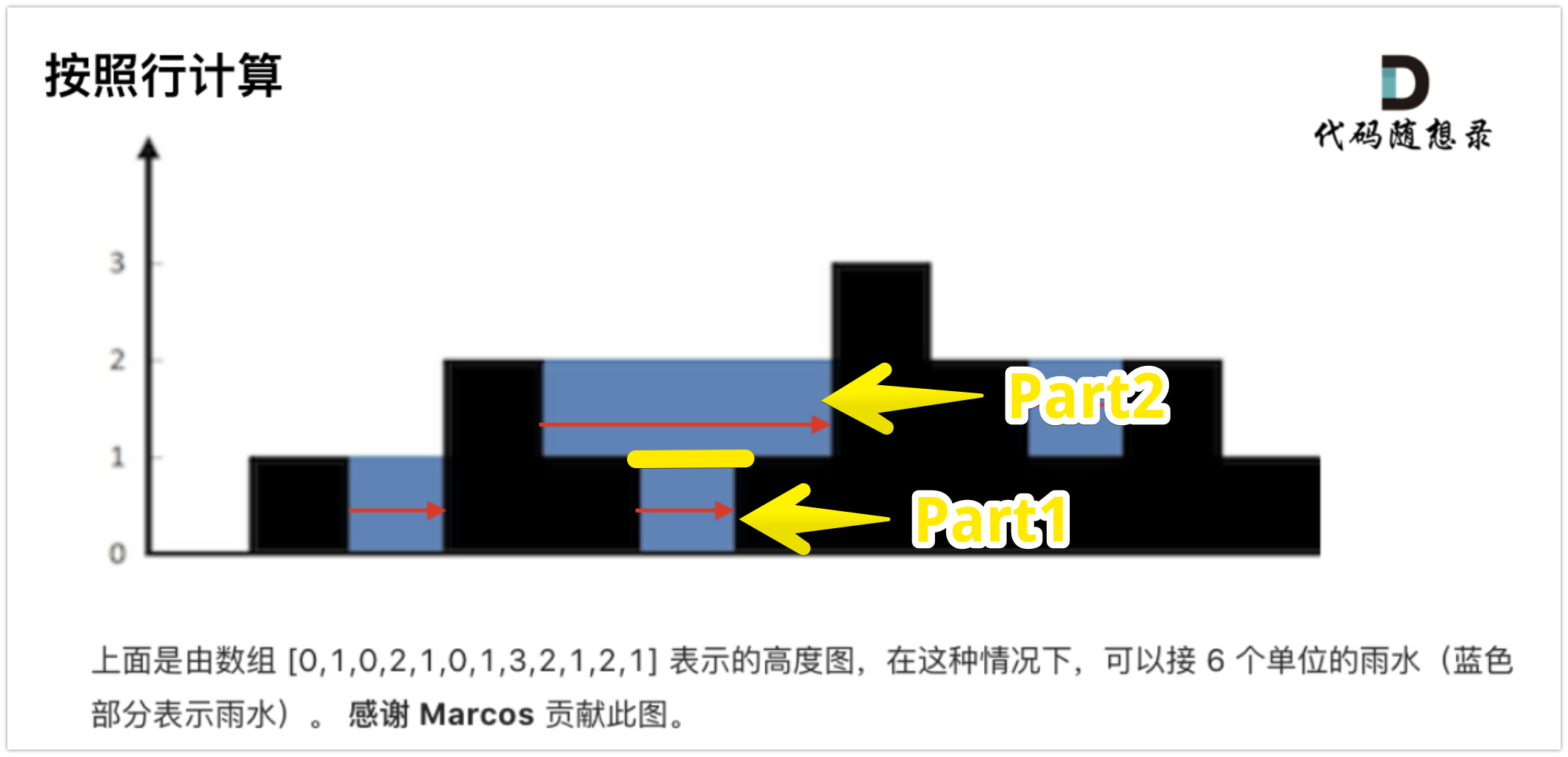
单调栈应该是单调递减栈,保存的元素应该是遍历过的元素内容,同之前每日温度题解 (opens new window)一样,这里也涉及入栈检查。即新遍历到的元素和栈顶元素的比较。
- 如果新元素比栈顶元素要大的话,就意味着栈顶元素能接水了(我们之前说过,栈是单调递减栈),所以我们就可以将栈顶元素 POP 出来,用新的栈顶元素和新元素去计算已经 POP 出来的元素在当下的接水量,即类似上图中的 Part1 部分。**值得注意的事这里的接水量并不是当前元素最终的接水量。**当然如果再次 POP 出来的值,依然比新元素小,我们就继续计算节水量,这时候计算的就是上面的 PART2 部分。这个过程不断循环,直到新元素比栈顶元素小或者栈为空。
- 新元素如果和栈顶元素相等的话,就直接入栈好了,因为等更大的元素来的时候也会同时计算这两者元素的接水量。
- 新元素如果比栈顶元素小的话直接入栈,构成单调递减栈。
完整代码如下,时间复杂度为 O(n),空间复杂度为 O(n)
func trap(_ height: [Int]) -> Int {
var res = 0
var stack = [Int]()
for (index,value) in height.enumerated() {
if stack.isEmpty == false {
var top = stack.last!
var topValue = height[top]
if value < topValue {
stack.append(index)
} else if value == topValue {
stack.append(index)
} else {
while stack.isEmpty == false && value > height[stack.last!] {
let mid = stack.removeLast()
if stack.isEmpty == false {
let minBtm = min(height[stack.last!], value)
//错误解法
//res = res + max(minBtm-height[mid], 0)
//正确解法
let h = max(minBtm-height[mid], 0)
let w = index - stack.last! - 1
res = res + h*w
}
}
stack.append(index)
}
} else {
stack.append(index)
}
}
return res
}
下面是精简判断条件的代码,精简判断条件后,感觉代码并不容易理解,所以随便看看就好了
func trap(_ height: [Int]) -> Int {
var res = 0
var stack = [Int]()
for (index,value) in height.enumerated() {
while stack.isEmpty == false && value > height[stack.last!] {
let mid = stack.removeLast()
if stack.isEmpty == false {
let minBtm = min(height[stack.last!], value)
let h = max(minBtm-height[mid], 0)
let w = index - stack.last! - 1
res = res + h*w
}
}
stack.append(index)
}
return res
}
# 总结
感觉用单调栈求解问题挺巧妙的,本质上确实是用空间换时间。
单调栈适用的场景也是求某个元素左右两侧的最大值,它的套路是,确定栈里存储的内容是什么,以及新遍历元素和栈顶元素的比较条件(也就是入栈检查要做好)。
这道题里单调栈的解法和每日温度的for循环里的判断条件几乎都是一模一样的,而且这两道题也是通过单调栈的解法,将时间复杂度从 O(n^2) 降低到 O(n)。
参考地址: